Marktforschung – Basiswissen > Stichprobengröße

Stichprobengröße

Stichprobengröße
– Definitionen, Erklärungen, Beispiele & Formeln

Die Stichprobengröße gibt die Anzahl der Elemente oder Einheiten an, die aus einer größeren Population ausgewählt werden, um Daten zu sammeln und Schlussfolgerungen über die Population zu ziehen. Eine ausreichend große Stichprobengröße ist notwendig, um eine repräsentative Stichprobe zu gewährleisten und eine genaue Schätzung der Parameter der Population zu ermöglichen.

Die Größe der Stichprobe ist ein wichtiger Faktor bei der Durchführung von Marktforschungsstudien. Eine ausreichend große Stichprobe gewährleistet eine repräsentative und zuverlässige Datenbasis. In diesem Blogbeitrag werden wir uns mit der Definition der Stichprobengröße, der Bestimmung der optimalen Stichprobe, den Formeln und Beispielen befassen.

Wichtige Fakten zur Stichprobengröße in der Übersicht

Diese Tabelle bietet einen schnellen Überblick über die wichtigsten Informationen in diesem Beitrag zum Thema Stichprobengröße.

Thema	Inhalte
Definition	Die Stichprobengröße ist die Anzahl der ausgewählten Elemente aus einer Population zur Datensammlung und zur Ableitung von Schlussfolgerungen über die Population. Eine ausreichend große Stichprobengröße ist entscheidend für die Repräsentativität und Genauigkeit der Ergebnisse.
Wichtigkeit der Stichprobengröße	Eine zu kleine Stichprobe kann ungenaue und nicht repräsentative Ergebnisse liefern. Eine ausreichend große Stichprobe gewährleistet Genauigkeit und minimiert Fehler und Verzerrungen. Die Stichprobengröße beeinflusst die statistische Signifikanz und Genauigkeit der Ergebnisse.
Berechnung der Stichprobengröße	Die Berechnung hängt von Faktoren wie Populationsgröße, Konfidenzniveau, Präzision, Heterogenität und verfügbaren Ressourcen ab. Es gibt verschiedene Formeln für unterschiedliche Arten von Stichproben (z.B., einfache Zufallsstichproben, proportionale Quotenstichproben).
Arten von Stichproben	Zufallsstichproben Quotenstichproben (proportional und disproportional) Klumpenstichproben (Einheitsklumpen und mehrstufige Klumpen)

Was ist eine Stichprobe und die Stichprobengröße

Eine Stichprobe ist eine zielgerichtete Auswahl von Elementen oder Individuen aus einer größeren Gruppe, sei es eine Bevölkerung, eine Datensammlung oder eine Zielgruppe. Sie wird verwendet, um Schlüsse über die gesamte Gruppe zu ziehen, ohne die gesamte Population zu untersuchen. Durch eine Stichprobe können Forscher kosteneffizient und zeitnah Daten sammeln, um Hypothesen zu testen oder Informationen zu gewinnen.

Die Stichprobengröße ist die Anzahl der Elemente in der Stichprobe. Sie ist von entscheidender Bedeutung, da sie die Genauigkeit und Verallgemeinerbarkeit der Ergebnisse beeinflusst. Eine zu kleine Stichprobe kann zu unzuverlässigen Schlüssen führen, während eine zu große Stichprobe unter Umständen Ressourcen verschwendet. Die Wahl der optimalen Stichprobengröße hängt von verschiedenen Faktoren ab, wie dem Studiendesign, den Merkmalen der Population und den Analysezielen. Es ist wichtig alle relevanten Faktoren sorgfältig zu berücksichtigen, wenn Sie die gewünschte Stichprobengröße mit Hilfe zuverlässiger Rechner oder Formeln bestimmen, die auf Ihre spezifischen Forschungsziele zugeschnitten sind.

Definition einer repräsentativen Stichprobe

Die Definition einer repräsentativen Stichprobe beinhaltet die Auswahl von Teilnehmern, die die untersuchte Population genau widerspiegeln. Dies kann durch eine sorgfältige Berechnung und Bestimmung von Faktoren wie Konfidenzniveau, Irrtumswahrscheinlichkeit (Fehlermarge) und Variabilität innerhalb der Grundgesamtheit erreicht werden. Die Verwendung von Hilfsmitteln wie z. B. Kalkulatoren kann bei der Bestimmung einer angemessenen Stichprobengröße helfen, um bei der Datenanalyse zuverlässige Ergebnisse zu erzielen.

Bei der Auswahl der richtigen Stichprobengröße für eine Studie ist es zudem entscheidend, geeignete Stichprobenauswahlverfahren wie die Zufallsstichprobe und die Quotenstichprobe zu berücksichtigen, um sicherzustellen, dass die Stichprobe repräsentativ ist und zuverlässige Ergebnisse liefert.
Bei der Zufallsstichprobe wird jeder Einheit in einer Population die gleiche Chance gegeben, ausgewählt zu werden. Im Gegensatz dazu werden bei der Quotenstichprobe bestimmte Merkmale wie Geschlecht oder Alter berücksichtigt und ein gewisses Verhältnis beibehalten.
Die Unterschiede zwischen den beiden Verfahren sollten sorgfältig abgewogen werden, bevor Sie sich für eines entscheiden.

Ziel

Um aussagekräftige Ergebnisse in der Marktforschung, zu erhalten, ist die Bestimmung einer ausreichenden Stichprobengröße unerlässlich. Eine angemessene Stichprobe erhöht nicht nur die Genauigkeit von Schätzungen, sondern minimiert auch Verzerrungen in den Ergebnissen durch eine adäquate Auswahl der Probanden. Daher sollte bei der Planung von Studien immer ein besonderes Augenmerk auf die Zielsetzung und Erweiterung der Stichprobe gelegt werden.

Warum ist die Stichprobengröße wichtig?

Die Stichprobengröße ist ein wichtiger Faktor in der Marktforschung. Eine zu kleine Stichprobe kann ungenaue Ergebnisse liefern, die nicht repräsentativ für die Gesamtbevölkerung sind. Um eine statistische Signifikanz zu erreichen und aussagekräftige Daten zu erhalten, sollten Forscher daher darauf achten, dass ihre Stichproben groß genug sind.

Eine ausreichende Stichprobengröße gewährleistet auch die Genauigkeit der Ergebnisse. Je größer die Stichprobe ist, desto geringer wird das Risiko von Fehlern oder Verzerrungen in den Daten. Daher ist es wichtig, bei der Planung von Marktforschungsstudien sorgfältig darüber nachzudenken, wie viele Teilnehmer benötigt werden, um aussagekräftige Ergebnisse zu erzielen.

Tipp:

Finden Sie die perfekten Umfrageteilnehmer für Ihre Forschungsprojekte bei resonio! Unser großer Teilnehmerpool steht Ihnen mit nur einem Klick zur Verfügung, um Ihre Stichprobengröße zu optimieren und Ihre Forschung zu bereichern.

Erfahren Sie mehr über unsere Umfrageteilnehmer

Statistische Signifikanz

Die Interpretation von p-Werten ist ein wichtiger Faktor bei der Bestimmung der statistischen Signifikanz von Studienergebnissen. Ein niedriger p-Wert zeigt an, dass die Wahrscheinlichkeit sehr gering ist, dass die beobachteten Ergebnisse zufällig sind. Es ist jedoch wichtig zu beachten, dass selbst ein signifikanter p-Wert nicht unbedingt bedeutet, dass eine starke Effektgröße vorliegt.

Die Berechnung der Effektgröße kann dazu beitragen, das Ausmaß des Unterschieds zwischen den Gruppen in einer Studie zu bestimmen. Dies kann nützlich sein, um festzustellen, ob die Ergebnisse klinisch oder praktisch relevant sind und somit für Entscheidungen im Bereich Marktforschung genutzt werden können. Es ist auch wichtig zu berücksichtigen, welche anderen Variablen möglicherweise einen Einfluss auf die Ergebnisse haben könnten und diese bei der Interpretation mit einzubeziehen.

Genauigkeit der Ergebnisse

Um die Genauigkeit der Ergebnisse bei der Durchführung einer Stichprobe in der Marktforschung sicherzustellen, ist es wichtig, das Konfidenzniveau zu bestimmen. Dieses Niveau gibt an, wie wahrscheinlich es ist, dass die Ergebnisse repräsentativ für die Gesamtheit sind. Zudem müssen potenzielle Fehlerquellen erfasst werden und geeignete Maßnahmen getroffen werden, um sie zu minimieren.

Die Genauigkeit hat Auswirkungen auf Entscheidungen, die auf Basis von Daten getroffen werden. Wenn eine Stichprobe nicht ausreichend groß oder unzureichend repräsentativ ist, können falsche Schlüsse gezogen und somit schlechte Entscheidungen getroffen werden. Eine sorgfältige Planung und Durchführung von Stichproben in der Marktforschung tragen daher maßgeblich zum Erfolg von Unternehmen bei.

Wie bestimme ich die optimale Stichprobengröße?

Nach der Formulierung der Forschungsfrage, sollten Sie die Größe Ihrer Stichprobe und den Stichprobenumfang bestimmen. Die Berechnung der optimalen Stichprobengröße hängt von verschiedenen Faktoren ab, darunter die Art Ihrer Studie, das gewünschte Signifikanzniveau und die erwartete Effektgröße.

Es ist wichtig zu beachten, dass eine größere Stichprobe nicht immer besser ist. Wenn bestimmte Faktoren berücksichtigt werden, kann eine kleinere Stichprobe ausreichen und genaue Ergebnisse liefern. In jedem Fall sollte die Auswahl der Stichprobengröße sorgfältig durchgeführt werden, um aussagekräftige Ergebnisse zu erhalten.

Berechnung der Stichprobengröße

Um eine aussagekräftige Stichprobe zu erhalten, müssen Sie zunächst die Grundgesamtheit definieren. Anschließend wählen Sie das Vertrauensniveau und den Fehlergrad aus. Die Standardabweichung oder Varianz sollten ebenfalls berücksichtigt werden.

Das Vertrauensniveau gibt an, wie sicher Sie sein möchten, dass die Ergebnisse Ihrer Stichprobe zutreffend sind. Der Fehlergrad bestimmt die maximale Abweichung der Schätzung vom tatsächlichen Wert in der Gesamtbevölkerung. Je höher das Vertrauensniveau und je geringer der Fehlergrad gewählt werden, desto größer wird Ihre notwendige Stichprobengröße sein.

Wählen Sie außerdem eine passende Methode zur Berechnung der Standardabweichungen oder Varianzen basierend auf Ihrer Datenverteilung und -struktur aus, um genaue Ergebnisse zu erzielen. Mit diesen Faktoren im Hinterkopf können Sie nun erfolgreich die Größe Ihrer benötigten Stichprobe berechnen.

Welche Faktoren beeinflussen die Stichprobengröße?

Die Stichprobengröße in der Marktforschung wird von verschiedenen Faktoren beeinflusst. Einige wichtige Faktoren sind:

Populationsgröße: Je größer die Population ist, desto größer muss die Stichprobe sein, um eine repräsentative Schätzung zu erhalten.
Konfidenzniveau: Je höher das Konfidenzniveau ist, desto größer muss die Stichprobe sein, um eine höhere Genauigkeit und Zuverlässigkeit der Ergebnisse zu gewährleisten.
Präzision: Je präziser das Ergebnis sein soll, desto größer muss die Stichprobe sein, um eine geringere Fehlerwahrscheinlichkeit zu erreichen.
Heterogenität der Population: Je heterogener die Population ist, desto größer muss die Stichprobe sein, um eine ausreichende Repräsentativität der verschiedenen Gruppen in der Population zu gewährleisten.
Variabilität: Je größer die Variabilität in der Population ist, desto größer muss die Stichprobe sein, um eine höhere Genauigkeit und Zuverlässigkeit der Ergebnisse zu gewährleisten.
Verfügbare Ressourcen: Die verfügbaren Ressourcen wie Zeit, Geld und Personal beeinflussen auch die Stichprobengröße. In vielen Fällen müssen Kompromisse zwischen der Stichprobengröße und den verfügbaren Ressourcen gemacht werden.

Stichprobengrößenrechner

Stichprobengröße berechnen

Konfidenzniveau

Fehlerspanne (%)

Bevölkerungsanteil (%)

Populationsgröße

Stichprobengröße: {{ sampleSize }}

Arten von Stichproben

Bei der Durchführung von Marktforschungsstudien ist es wichtig, die richtige Stichprobengröße zu bestimmen. Es gibt verschiedene Arten von Stichproben, aus denen Forscher wählen können, um ihre Studien durchzuführen. Dazu gehören Zufallsstichproben, Quotenstichproben und Klumpenstichproben.

Zufallsstichproben sind eine zufällige Auswahl von Teilnehmern aus einer bestimmten Population. Quotenstichproben hingegen werden verwendet, um sicherzustellen, dass die Merkmale der Teilnehmer in Bezug auf Geschlecht oder Alter mit den Eigenschaften der gesamten Population übereinstimmen. Schließlich werden bei Klumpenstichproben Gruppen von Personen als Einheit ausgewählt und dann befragt. Die Wahl der passenden Art von Stichprobe hängt vom Ziel und Kontext Ihrer Studie ab.

Zufallsstichproben

Für Marktforscher sind Zufallsstichproben ein wichtiger Bestandteil der Datenerhebung. Eine einfache Zufallsstichprobe ist die grundlegendste Form, bei der jedes Element einer Population gleichermaßen die Chance hat, ausgewählt zu werden. Bei einer geschichteten Zufallsstichprobe wird die Population in verschiedene Schichten unterteilt und eine Stichprobe wird aus jeder Schicht gezogen, um sicherzustellen, dass jede Gruppe innerhalb der Bevölkerung berücksichtigt wird. Die Mehrfachauswahl-Zufallsstichprobe ermöglicht es den Probanden in mehreren Gruppen oder Kategorien gleichzeitig eingeschlossen zu werden und findet oft Anwendung bei Studien zur Kundenzufriedenheit oder Produktpräferenzen.

Formel zur Berechnung der Stichprobengröße für die einfache Zufallsstichprobe

Die Formel zur Berechnung der Strichprobengröße bei der einfachen Zufallsstichprobe lautet:
n = (Z^2 * p * q) / e^2

Dabei steht n für die Strichprobengröße, Z für den Z-Score, der mit dem gewünschten Konfidenzniveau und der Fehlerwahrscheinlichkeit verbunden ist, p für die erwartete Erfolgsrate in der Population, q für die erwartete Misserfolgsrate in der Population und e für die zulässige Fehlerquote.

Um beispielsweise eine Strichprobengröße für eine Population von 1000 Personen mit einem Konfidenzniveau von 95% und einer erwarteten Stichprobenabweichung von 5% zu berechnen, könnte man folgende Formel verwenden:

n = (1.96^2 * 0.5 * 0.5) / (0.05^2) = 384.16

Daher würde eine Stichprobe von mindestens 385 Personen ausgewählt werden, um eine repräsentative Schätzung der zugrunde liegenden Population zu erhalten.

Quotenstichproben

Für Marktforscher sind Quotenstichproben ein wichtiger Bestandteil ihrer Arbeit. Es gibt zwei Arten von die proportionale und disproportionale. Die proportionale Quotenstichprobe wird verwendet, wenn alle Merkmalsausprägungen in der Grundgesamtheit gleich häufig vorkommen. Bei der disproportionalen Variante hingegen werden bestimmte Merkmalsausprägungen gezielt überrepräsentiert.

Formel zur Berechnung der Stichprobengröße für die proportionale Quotenstichprobe
Die Berechnung der Strichprobengröße bei einer proportionalen Quotenstichprobe ist ähnlich wie bei einer einfachen Zufallsstichprobe und einer Quotenstichprobe, aber die Formel muss angepasst werden, um die proportionale Auswahl der Stichprobe zu berücksichtigen.
Die Formel zur Berechnung der Strichprobengröße bei proportionalen Quotenstichproben lautet:
n = (Z^2 * p * q * N) / [(Z^2 * p * q * N) + ((N – 1) * e^2)]
Dabei steht n wieder für die Strichprobengröße, Z für den Z-Score, der mit dem gewünschten Konfidenzniveau und der Fehlerwahrscheinlichkeit verbunden ist, p und q für die erwarteten Anteile der Merkmalsausprägungen in der Population, N für die Größe der Population und e für die zulässige Fehlerquote.
Um beispielsweise eine Strichprobengröße für eine Population von 1000 Personen mit einem Konfidenzniveau von 95%, einer erwarteten Stichprobenabweichung von 5%, einer erwarteten Merkmalsausprägung von 50% und einer zulässigen Fehlerquote von 3% zu berechnen, könnte man folgende Formel verwenden:
n = (1.96^2 * 0.5 * 0.5 * 1000) / [(1.96^2 * 0.5 * 0.5 * 1000) + ((1000 – 1) * 0.03^2)] = 265.18
Daher würde eine Stichprobe von mindestens 266 Personen proportional zu den Anteilen der Merkmalsausprägungen in der Population ausgewählt werden, um eine repräsentative Schätzung der zugrunde liegenden Population zu erhalten. Es ist wichtig zu beachten, dass die proportionale Auswahl der Stichprobe sicherstellt, dass die Stichprobe die Merkmalsausprägungen der Population angemessen widerspiegelt.
Formel zur Berechnung der Stichprobengröße für die disproportionale Quotenstichprobe
Die disproportionale Quotenstichprobe ist eine weitere spezielle Art der Quotenstichprobe, bei der die Stichprobe nicht proportional zu den Anteilen der Merkmalsausprägungen in der Population ausgewählt wird, sondern bestimmte Merkmalsausprägungen überrepräsentiert sind. Die Berechnung der Strichprobengröße bei einer disproportionalen Quotenstichprobe ist ähnlich wie bei einer proportionalen Quotenstichprobe, aber die Formel muss angepasst werden, um die disproportionale Auswahl der Stichprobe zu berücksichtigen.
Die Formel zur Berechnung der Strichprobengröße bei disproportionalen Quotenstichproben lautet:
n_j = (Z^2 * p_j * q_j * N) / [(Z^2 * p_j * q_j * N) + ((N – 1) * e^2 * sum(w_j^2))]
Dabei steht n_j für die Stichprobengröße der jeweiligen Merkmalsausprägung j, Z für den Z-Score, der mit dem gewünschten Konfidenzniveau und der Fehlerwahrscheinlichkeit verbunden ist, p_j und q_j für die erwarteten Anteile der Merkmalsausprägungen in der Population für die jeweilige Ausprägung j, N für die Größe der Population und e für die zulässige Fehlerquote. Zudem kommt der Faktor w_j hinzu, welcher die Über- oder Unterrepräsentation der jeweiligen Merkmalsausprägung j in der Stichprobe angibt. Wenn beispielsweise die Merkmalsausprägung A überrepräsentiert sein soll, wird w_A größer als 1 sein.
Um beispielsweise eine disproportionale Quotenstichprobe für eine Population von 1000 Personen mit einem Konfidenzniveau von 95%, einer erwarteten Stichprobenabweichung von 5%, einer erwarteten Merkmalsausprägung von 50% und einer zulässigen Fehlerquote von 3% zu berechnen, könnte man folgende Formel verwenden:
n_A = (1.96^2 * 0.7 * 0.3 * 1000) / [(1.96^2 * 0.7 * 0.3 * 1000) + ((1000 – 1) * 0.03^2 * 2^2)]
n_B = (1.96^2 * 0.4 * 0.6 * 1000) / [(1.96^2 * 0.4 * 0.6 * 1000) + ((1000 – 1) * 0.03^2 * 0.5^2)]
n_C = (1.96^2 * 0.2 * 0.8 * 1000) / [(1.96^2 * 0.2 * 0.8 * 1000) + ((1000 – 1) * 0.03^2 * 0.5^2)]
Dabei soll beispielsweise Merkmalsausprägung A in der Stichprobe doppelt so häufig vorkommen wie in der Population, Merkmalsausprägung B soll gleich häufig vorkommen wie in der Population und Merkmalsausprägung C soll halb so häufig vorkommen wie in der Population.
Die berechneten Stichprobengrößen würden dann wie folgt aussehen:
n_A = (1.96^2 * 0.7 * 0.3 * 1000) / [(1.96^2 * 0.7 * 0.3 * 1000) + ((1000 – 1) * 0.03^2 * 2^2)] = 96
n_B = (1.96^2 * 0.4 * 0.6 * 1000) / [(1.96^2 * 0.4 * 0.6 * 1000) + ((1000 – 1) * 0.03^2 * 0.5^2)] = 179
n_C = (1.96^2 * 0.2 * 0.8 * 1000) / [(1.96^2 * 0.2 * 0.8 * 1000) + ((1000 – 1) * 0.03^2 * 0.5^2)] = 120
Wie man sieht, sind die Stichprobengrößen je nach Über- oder Unterrepräsentation der Merkmalsausprägungen unterschiedlich. Wenn man beispielsweise eine Stichprobe mit einer fixen Größe von 300 Personen ausgewählt hätte, wäre es nicht möglich gewesen, die Vorgaben bezüglich der disproportionalen Auswahl der Merkmalsausprägungen zu erfüllen. In diesem Fall ist es also wichtig, die Stichprobengröße auf Basis der spezifischen Anforderungen an die disproportionale Quotenstichprobe zu berechnen.

Klumpenstichproben / Cluster-Stichprobe

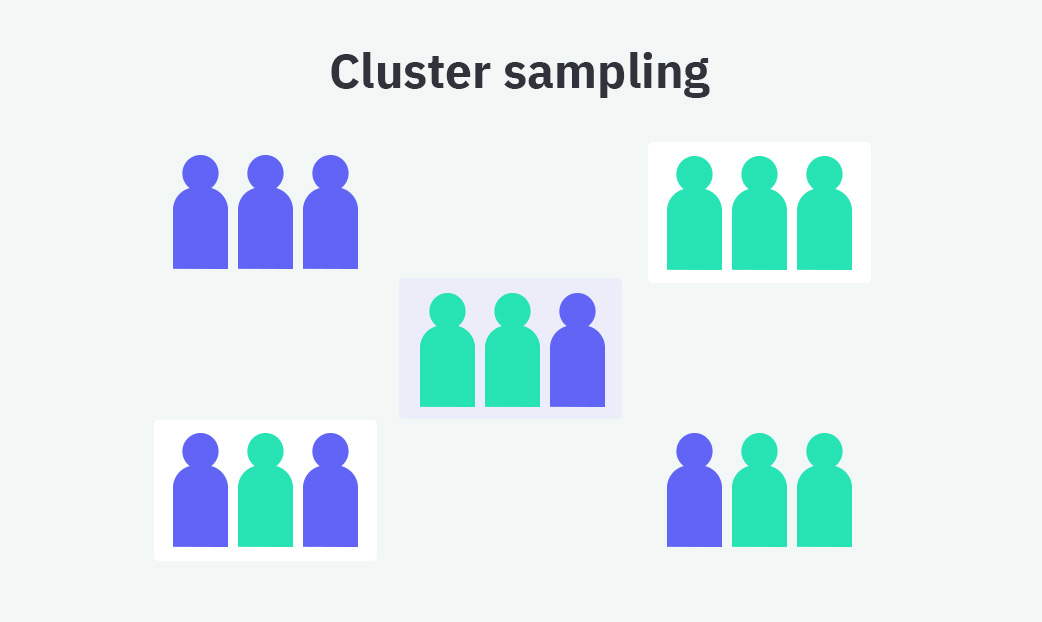
Für die Auswahl von Klumpenstichproben (häufig auch als Cluster-Stichprobe bezeichnet) gibt es zwei Verfahren: das Einheitsklumpen-Stichprobenauswahlverfahren und das mehrstufige Klumpenauswahlsystem. Beim Einheitsklumpen-Verfahren werden alle Elemente in der Population zu gleichen Gruppen zusammengefasst, bevor zufällig eine bestimmte Anzahl an Gruppen ausgewählt wird. Das mehrstufige System hingegen wählt zunächst zufällig einige Übergruppen, aus denen dann weitere Untergruppen gewählt werden.

Das Ziel beider Methoden ist es, eine repräsentative Stichprobe für die gesamte Population zu erhalten. Die Wahl des Verfahrens hängt dabei von den spezifischen Gegebenheiten der Studie ab und sollte sorgfältig durchdacht werden.

Formel zur Berechnung der Stichprobengröße mit dem Einheitsklumpen-Stichprobenauswahlverfahren
Beim Einheitsklumpen-Stichprobenauswahlverfahren wird die Stichprobe durch die Auswahl von zufällig ausgewählten Einheiten (auch Cluster genannt) gebildet, die aus mehreren Elementen bestehen. Das Verfahren wird typischerweise angewendet, wenn es schwierig oder kostspielig ist, jedes Element in der Population zu identifizieren und auszuwählen.
Um die Stichprobengröße bei diesem Verfahren zu berechnen, müssen zunächst die Anzahl der Cluster (k) und die Anzahl der Elemente in jedem Cluster (m) bekannt sein.
Anschließend kann die Stichprobengröße (n) mit der folgenden Formel berechnet werden:
n = k * m * deff
wobei deff der sogenannte Design-Effekt ist, der die erhöhte Varianz in der Stichprobe aufgrund der Clusterverarbeitung berücksichtigt. Der Design-Effekt kann aus früheren Studien oder Schätzungen abgeleitet werden. Wenn keine früheren Informationen verfügbar sind, kann deff grob geschätzt werden, indem man die durchschnittliche Clustergröße (m) schätzt und die Intraklassenkorrelationskoeffizienten (ICC) in Betracht zieht. Die ICC-Werte geben an, inwieweit die Elemente innerhalb eines Clusters ähnlicher sind als die Elemente in anderen Clustern.
Die Formel zur Schätzung des Design-Effekts lautet:
deff = 1 + (m-1) * ICC
Die Gesamtstichprobengröße kann dann unter Berücksichtigung der gewünschten Präzision der Stichprobe und des Konfidenzniveaus durch Anpassen der Anzahl der Cluster (k) oder der Anzahl der Elemente pro Cluster (m) angepasst werden.
Formel zur Berechnung der Stichprobengröße mit dem mehrstufigen Klumpenauswahlsystem
Das mehrstufige Klumpenauswahlsystem ist eine Erweiterung des Einheitsklumpen-Stichprobenauswahlverfahrens und wird typischerweise angewendet, wenn es in der Population mehrere Hierarchieebenen gibt. Bei diesem Verfahren werden mehrere Klumpenebenen ausgewählt, um die Stichprobe zu bilden.
Die Berechnung der Stichprobengröße in einem mehrstufigen Klumpenauswahlsystem hängt von der Anzahl der Klumpenebenen und der Anzahl der Elemente in jedem Cluster in jeder Hierarchieebene ab. Wenn die Stichprobengröße (n) und die Anzahl der Hierarchieebenen (k) bekannt sind, kann die durchschnittliche Clustergröße in der obersten Ebene (m1) berechnet werden.
Anschließend kann die Gesamtstichprobengröße (N) mit der folgenden Formel berechnet werden:
N = m1 * m2 * … * mk * deff
wobei m2 bis mk die durchschnittliche Clustergröße in jeder Hierarchieebene darstellen und deff der Design-Effekt ist, der die erhöhte Varianz in der Stichprobe aufgrund der Clusterverarbeitung berücksichtigt. Der Design-Effekt kann durch frühere Studien oder Schätzungen abgeleitet werden.
Wenn keine Informationen zur durchschnittlichen Clustergröße oder zum Design-Effekt verfügbar sind, kann deff durch eine Schätzung der Intraklassenkorrelationskoeffizienten (ICC) in jeder Hierarchieebene berechnet werden. Die ICC-Werte geben an, inwieweit die Elemente innerhalb eines Clusters ähnlicher sind als die Elemente in anderen Clustern.
Der Design-Effekt kann dann wie folgt berechnet werden:
deff = 1 + (m1-1) * ICC1 + (m1 * (m2-1)) / 2 * ICC2 + …
Die Gesamtstichprobengröße kann dann unter Berücksichtigung der gewünschten Präzision der Stichprobe und des Konfidenzniveaus durch Anpassen der Anzahl der Cluster in jeder Hierarchieebene oder der Anzahl der Elemente pro Cluster in jeder Hierarchieebene angepasst werden.

Fazit

In der Marktforschung spielt die Stichprobengröße eine entscheidende Rolle für die Validität der Ergebnisse. Eine zu kleine Stichprobe kann zu verfälschten Resultaten führen, während eine zu große Stichprobe unnötige Kosten verursachen kann. Es ist wichtig, den angemessenen Umfang entsprechend des Forschungsziels auszuwählen und Fehlermöglichkeiten bei statistischen Auswertungen zu berücksichtigen.

Um genaue und aussagekräftige Daten in der Marktforschung zu erhalten, sollten Forscher sorgfältig die Größe ihrer Stichproben planen. Das bedeutet, nicht nur das Ziel ihrer Untersuchung im Auge zu behalten, sondern auch mögliche Fehlerquellen bei der Analyse mit einzubeziehen. Durch diese Vorgehensweise können fundierte Entscheidungen auf Basis validierter Daten getroffen werden.

Erfahren Sie mehr zur Zielgruppen-Segmentierung

FAQs zur Stichprobengröße

Was ist die Stichprobengröße?

Die Stichprobengröße bezieht sich auf die Anzahl der Elemente in einer Stichprobe, die aus einer Gesamtmenge von Elementen ausgewählt wird. In der Statistik ist die Stichprobengröße ein wichtiger Faktor, der bestimmt, wie genau die Ergebnisse einer Stichprobe die tatsächlichen Eigenschaften der Gesamtmenge widerspiegeln können.

Warum ist die Stichprobengröße wichtig?

Die Stichprobengröße ist wichtig, weil sie einen direkten Einfluss auf die Genauigkeit und Zuverlässigkeit der Ergebnisse hat. Je größer die Stichprobe ist, desto genauer und zuverlässiger sind die Ergebnisse. Wenn die Stichprobe zu klein ist, können die Ergebnisse ungenau und nicht repräsentativ sein.

Wie bestimmt man die Stichprobengröße?

Die Bestimmung der Stichprobengröße hängt von verschiedenen Faktoren ab, wie z.B. dem Zweck der Studie, der Art der Daten, der erwarteten Präzision und dem verfügbaren Budget. Es gibt verschiedene statistische Methoden, um die optimale Stichprobengröße zu berechnen, wie z.B. die einfache Zufallsstichprobe oder die stratifizierte Stichprobe.

Was passiert, wenn die Stichprobengröße zu klein ist?

Wenn die Stichprobengröße zu klein ist, kann dies zu ungenauen und nicht repräsentativen Ergebnissen führen. Eine zu kleine Stichprobe kann auch zu einer erhöhten Wahrscheinlichkeit von Stichprobenverzerrungen führen, wie z.B. der Selektionsverzerrung oder der Stichprobenauswahlverzerrung. Daher ist es wichtig, die Stichprobengröße sorgfältig zu planen und zu bestimmen.

Wie beeinflusst die Stichprobengröße die statistische Signifikanz?

Die Stichprobengröße hat einen direkten Einfluss auf die statistische Signifikanz. Je größer die Stichprobengröße ist, desto wahrscheinlicher ist es, dass Unterschiede zwischen Gruppen oder Variablen statistisch signifikant sind. Eine zu kleine Stichprobe kann jedoch dazu führen, dass Unterschiede nicht signifikant sind, selbst wenn sie tatsächlich existieren. Daher ist es wichtig, eine angemessene Stichprobengröße zu verwenden, um die statistische Signifikanz zu gewährleisten.